3D Math Basics, Vectors, Direction, Distance

One of the most useful forms of math to be used in the UDK is 3D vector math. Frequently, we need to be able to plot and modify coordinates given existing coordinates in a 3D environment. We also need to be able to orient various objects towards and away from each other. We use vector, rotator, and quaternion math for this. This notes section will deal with the basics of vector math, including vector subtraction, as well as directioning and rotators.

Dimensions

A dimension is a degree of freedom. This concept is not intuitive but it can be related to the real world in order to better grasp it. For example, in the real world, we have 3 spatial dimensions and 1 time dimension (at minimum). Since we are only dealing with spatial quantities, let's disregard the time dimension. This leaves us with 3 spatial dimensions.

If we think of the real world universe as a huge box, we can represent positions along its width with a dimension, we can call this dimension X; positions along its length can also have a dimension, let's call this one Y; finally we will use a dimension to plot positions along the box's height, we will call this dimension Z.

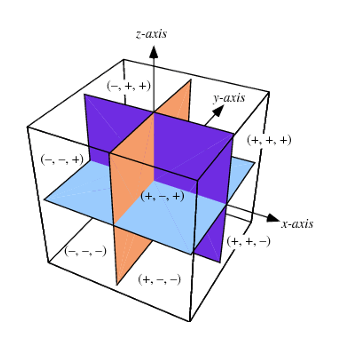
Now there are some complications to this example, like the fact that depending on the viewer's current rotation, width, length, and height may have different directions. This is solved by the fact that all virtual worlds that use this type of position information always have a canonical rotation, which is the one original rotation that the world has; its neutral rotation, if you will. The width, length, and height of the universe are always interpreted with this rotation in mind.

Vectors then describe a specific point in this universe. We examine vectors in the following section.

Vector Position

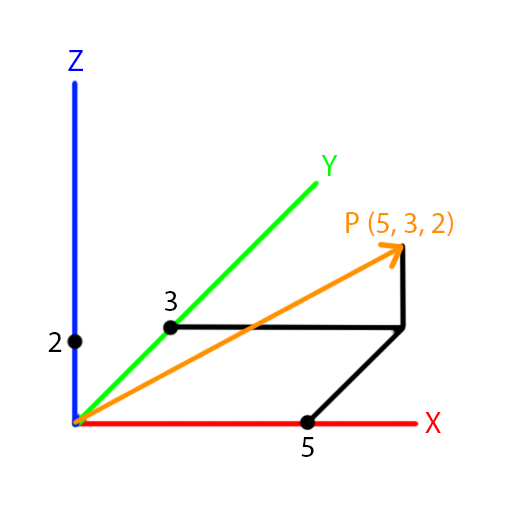
A vector is a mathematical quantity that represents a position along multiple dimensions. That is why vectors are typed by the number of dimensions that they encompass. The following are some common vector types:

• Vector 1, storing 1 dimensional position, eg X
• Vector 2, storing 2 dimensional positions, eg X, Y
• Vector 3, storing 3 dimensional positions, eg X, Y, Z

In the UDK, the type vector is a Vector 3 since it has 3 dimensions. It is ideal for describing coordinates in the UDK world. For example, a vector that holds the values X:+5, Y:+3, Z:+2 is a vector that describes a position in the world that is:

• 5 units along the positive X axis from the origin of the world
• 3 units along the positive Y axis from the origin of the world
• 2 units along the positive Z axis from the origin of the world

You may have noticed use of the term origin. The origin of the world is simply the vector (0, 0, 0).

UDK, Declaration

The type used to store a vector in the UDK is vector. It can be used as follows:

var vector MemberVectorA;
var vector MemberVectorB;
local vector LocalVector;

Like any other variable type, we can declare a variable as a member variable or as a local variable. We can initialize a vector declared as a member variable by using parenthesis syntax. For example:

Defaultproperties
{
    MemberVectorA=(X=10,Y=3,Z=7)
    MemberVectorB=(Z=6)
}

In this case, we initialized MemberVectorA to a vector with an X component of 10, Y component of 3, and Z component of 7. Similarly, we initialized MemberVectorB to a vector with an X and Y component of 0, and a Z component of 6. When using parenthesis initialization syntax, any component not mentioned is set to 0.

UDK, Assignment

As you would expect, we can assign to/from vectors. We can read and write to individual vector components, ie:

local vector ExampleVector;
local float ExampleFloat;

ExampleVector.X = 10;
ExampleVector.Y = 62;
ExampleFloat = ExampleVector.Y;

In this case, we set the X and Y components of ExampleVector to 10 and 62, respectively. Then, we read the Y component and assign it to ExampleFloat; in this case, ExampleFloat's final value is 62. Notice that we did not assign anything to ExampleVector's Z component; by doing so, we leave the value at 0. In UnrealScript, all variables initialize to 0 or the equivalent of 0.

We can also assign whole vectors:

local vector A, B;

A.X = 64;
A.Z = 73;
B = A;

In this case, we assign 64 to A's X component and 73 to A's Z component. This means that A's XYZ components currently hold the values 64, 0, 73. We then assign B to A. By the end of the segment, both vectors now hold the values 64, 0, 73.

As a convenience, we can create and assign vector literals by using the function vect. For example:

local vector A;
A = vect(10, 0, 20);

In this case, A now holds the XYZ values 10, 0, 20. Note that the vect keyword cannot be passed variables; it must be passed float literals. For example, the following would be a syntax error:

local vector A;
local float X;

X = 10;
A = vect(X, 0, 20);  // Syntax error, cannot pass variable to vect

Vector Scaling

One of the most important operations that could be performed on a vector is scaling. A vector can be scaled by a float by multiplying each of its components by the floating point value. For example:

Given the vector X:2, Y:4, Z:6, we could do the following:

(2, 4, 6) * 3 = (6, 12, 18)
(2, 4, 6) * 0.5 = (1, 2, 3)

The result of multiplying a vector by a floating point value is another vector. This operation allows us to linearly magnify or shrink a vector.

UDK, Float Multiplication

In the UDK, float multiplication is done naturally. For example:

local vector A, B, C;

A = vect(2, 4, 6);
B = A * 2;
C = A * 0.5;

The result of this code is that the vector B will hold the value (4, 8, 12) while the vector C will hold the value (1, 2, 3).

Vector Length

It can be useful to find the length of a vector. This is done by using the pythagorean theorem, applying it twice to find the length of a vector. As a reminder, the pythagorean theorem as follows:

Let A and B be the lengths of the non-hypotenuse sides of a right angle triangle.
Let C by the length of the hypotenuse of the same right angle triangle.

Then:
A^2 + B^2 = C^2

We can use this to find the length of our vector from the example before:

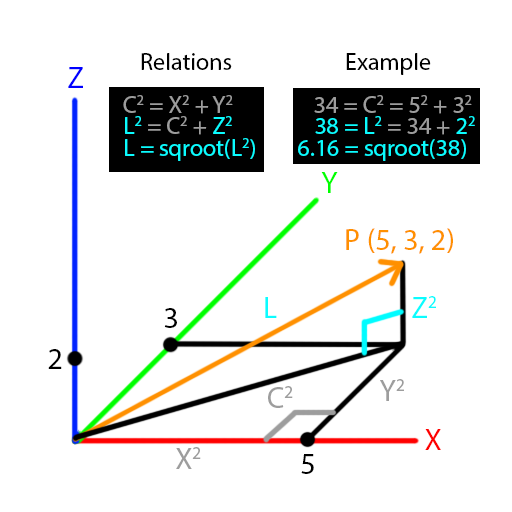
In the above example, we can form two right angle triangles:

• The grey triangle flat on the base, formed between the X and Y components
• The cyan triangle upright, formed between the Z component and the hypotenuse from the grey triangle

So with the pythagorean theorem in mind, we can:

1. Find the squared length of the hypotenuse of the grey triangle
2. Use the squared length of the hypotenuse from the last calculation in finding the squared length of the hypotenuse of the cyan triangle

Once we have the squared length of the hypotenuse of the cyan triangle, we can take the square root to get the length of the hypotenuse of the cyan triangle, which is equivalent to the length of the vector.

So, our final equation looks like: length(vector) = sqroot(vector.X^2 + vector.Y^2 + vector.Z^2)

UDK, Length or Size

We use the function VSize to find the length of a vector in the UDK. It is defined in object.uc as follows:

native(225)        static final function    float    VSize        ( vector A );

Notice that this function accepts a vector and returns a float. The returned value is the length of the vector. For example, given our vector in the picture above:

local float sz;

sz = vsize(vect(5, 3, 2));

After this piece of code, sz will contain the value 6.16.....

Vector Direction, Normalization

Since we've extracted length from a vector, we can also extract direction from a vector. A direction vector is nothing more than a vector with a size of 1. We call this type of vector a unit vector.

So why 1? Why is that size significant? Why not 2, or 63? The reason is that a size 1 vector can be multiplied by any float to generate a vector with the same direction, sized at exactly the value of the float.

We can get a size 1 vector from any existing vector (except the vector (0, 0, 0) ) by dividing each of the components of the vector by the size of the vector. For example, given our previous example vector, we can find a direction vector as:

exampleVector = (5, 3, 2)
length = 6.16...
direction     = (5 / 6.16..., 3 / 6.16..., 2 / 6.16...) = (0.81..., 0.49..., 0.32...)

We get the approximate direction vector (0.81, 0.49, 0.32). Visually, this looks like:

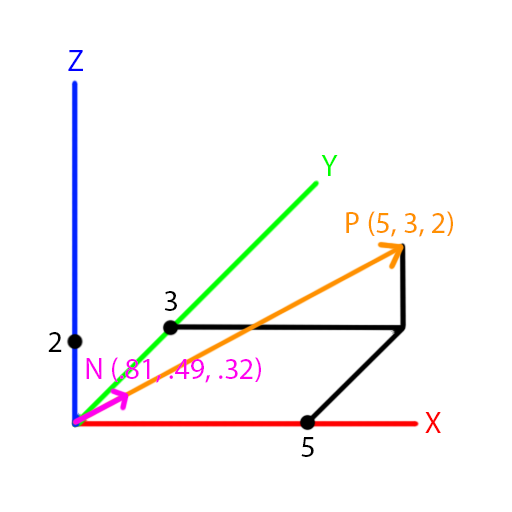
We call this process, vector normalization; the idea is that a normalized vector is a vector whose length is exactly equal to 1.

UDK, Normal

To get a normal vector in the UDK, we use the Normal function. It is defined in object.uc as follows:

native(226)        static final function    vector    Normal        ( vector A );

This can be used as follows:

local vector A;

A = normal(vect(5, 3, 2));

In this case, A will be approximately equivalent to the vector (0.81, 0.49, 0.32).

Vector Addition, Subtraction

We can add and subtract vectors from each other. Addition and subtraction in vectors function similarly to how they do with scalar floating point values. That is, the following relations are held:

If A + B = C, then A = C - B

If we substitute some float scalars above, we see that this naturally holds:

2 + 3 = 5, then 2 = 5 - 3

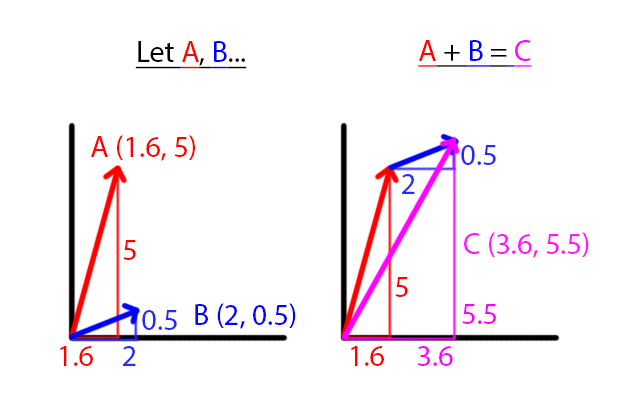
When adding and subtracting vectors, we simply apply the operations on each component, respectively. For example:

(1, 2, 3) + (4, 5, 6) = (5, 7, 9), then (1, 2, 3) = (5, 7, 9) - (4, 5, 6)

Visual Addition

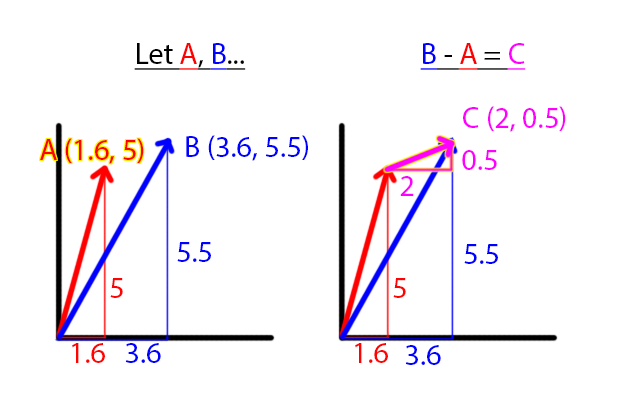
Visual Subtraction

UDK, Add/Subtract Operators

This functions as you would expect in the UDK:

local vector A, B, C, D;

A = vect(1, 2, 3);
B = vect(4, 5, 6);
C = A + B;
D = C - B;

at the end of the above segment, C holds the value (5, 7, 9) and D holds the value (1, 2, 3).

Vector Subtract For Orientation

Since:

• Vectors can be used as coordinates
• The relationship "C - B = A, therefore A + B = C" holds

Notice the following visual phenomenon:

In the picture above, adding the green vector to the A vector, results in the B vector. Therefore, B - A = green vector. We can use this relationship to find a vector that travels from a source coordinate to a destination coordinate. We can use this in a number of very useful ways:

Getting Offset Vector

An offset vector is a vector that when added to a source vector, will move it by a certain amount. For example, to get a vector that transforms a given vector A to a given vector B when added to A, we simply subtract B from A. For example:

Source = (1, 2, 3)
Destination = (10, 10, 10)
Offset = Destination - Source = (10, 10, 10) - (1, 2, 3) = (9, 8, 7)

Now notice that:
Source + Offset = Destination

So:
(1, 2, 3) + (9, 8, 7) = (10, 10, 10)

Getting Distance

If we can generate a vector that travels from a source to a destination, we can get the distance between those two points by finding the length of the offset vector. For example:

Source = (1, 2, 3)
Destination = (10, 10, 10)
Offset = Destination - Source = (10, 10, 10) - (1, 2, 3) = (9, 8, 7)
Distance = length(9, 8, 7) = 13.93.....

Getting Direction Vector

A direction vector is similar to an offset vector but is sized 1. It is useful when we don't need the distance.

Use this when you need to:

1. When you are doing some vector math and the functions you are using don't tolerate vectors with a size other than 1
2. When you need to get a vector in a particular direction but sized the same as another vector, eg when rotating vectors

This is done by taking the normal of the offset vector. For example:

Source = (1, 2, 3)
Destination = (10, 10, 10)
Offset = Destination - Source = (10, 10, 10) - (1, 2, 3) = (9, 8, 7)
Distance = length(9, 8, 7) = 13.93.....
Direction = normal(offset) = (9, 8, 7) / 13.93... = (0.65..., 0.57..., 0.5...)